In this post I'm going to describe a new metric Power Index, which is used to find maximal efforts in general data without any knowledge of an athlete and a Submaximal Effort Filtering Algorithm using a modified form of a convex hull search algorithm. These approaches were developed to support the implementation of the Banister IR model in GoldenCheetah.
And it should be no surprise that performance tests are the main inputs into most performance models. If we want to model and predict maximal performance, generally we need a measure of maximal effort from a performance test.
One way of overcoming this is to design an approach for modelling performance that doesn't need maximal tests. The TrainingPeaks Performance Manager Chart takes this approach. It is based upon the Banister Impulse Response model and provides a measure of likely performance called CTL and measure of likely fatigue called TSB. These measures are related only to the accumulated training load over a long and short duration. Effectively comparing how much training you've been doing over the long haul versus the last few days. Increase load too quickly and you'll fatigue and risk injury, reduce it too much and you'll recover quickly but lose fitness.
By contrast, Banister fits and correlates accumulated training load to performance tests, these are typically 6 minute TTE tests but it can use any measure. It then predicts future performance given a future training load using the coefficients from the fitting process.
These coefficients are effectively what were removed from Banister model to create the PMC. Of course, by doing so this removed the ability to make predictions about future performance. This is fine for tracking overall progression but is rather abstract given the units used don't relate to performance. As a result some coaches try to assign meaning to aspects of the PMC that is akin to tasseography.
Banister is a much more useful tool since it can track progression in concrete terms and predict future performance by learning from our past response. The Banister model isn't perfect and has issues too, one of the biggest is the need for those pesky performance tests.
So, what we really need is a way of using the Banister approach, but without necessarily mandating regular performance testing.
I previously blogged about finding sustained efforts in a ride, using a PD model to hunt them down. Well, finding a maximal effort takes a similar approach. Only this time I'm not going to need to know anything about the athlete. I need to extract these maximal efforts purely from the raw data.
That's what this blogpost is going to describe, eventually.
We all know that some cyclists have a better sprint than others, some are better at time-trialling and some seem to be more punchy or better at climbing. So much so that cycling has a lexicon to describe them; 'sprinteurs', 'rouleurs', 'puncheurs' and 'grimpeurs'. Putting weight and height to one side, ultimately the athlete type is characterised by the shape of their power duration curve. Sprinters typically have a high Pmax and W', TTers have a high CP regardless of weight, puncheurs maintain high power for much longer.
So, around Christmas 2018, Mike downloaded the MMP data for all the athletes in the GC opendata set (around 2,500 seasons of a 100 or more workouts) and performed a Functional Principal Component Analysis on them.
The analysis identified 3 parts of the PD relationship that explain over 90% of the variation in all cyclists. The aspects that differentiate the rouleurs, puncheurs and so on. They are:
I also found the average (male) athlete; a Critical Power of 261w, a W' of 15.5kj and a Pmax of 1100w.
The Power Index of any power duration point will tell us, it is effectively the same thing as the PC1 from the FPCA above.
It is the power for the interval duration expressed as a percentage of the predicted power for the same interval duration we get for the average athlete.
The prediction can come from any PD model, it doesn't matter too much so long as the PD model is relatively reliable. For the implementation in GC I used the Morton 3 parameter model. I could avoid a model altogether and use the 50th quartile MMP data from the Opendata analysis. But using a model is quick and easy enough to implement.
So as a worked example, lets look at the 3 intervals above, and see how they come out. First, to predict power for an interval with duration t:
So plugging the numbers into the formula, the predicted power for 4, 10 and 20 minute intervals, for our average athlete (CP=261w, W'=15.5kj, Pmax=1100w) are shown below, along with the average powers from above, the calculated power index percentage and rank:
The 4min effort is the best, but those 10 and 20minute efforts are a close run thing. In practice, to isolate the impact of the other principal components it only makes sense to work with intervals between 3 and 20 minutes. Which rather helpfully maps quite nicely onto the CP models. So, in summary we have a metric that can be used to rank intervals between 3 and 20 minutes to extract the very best efforts.
One other aspect of this is quite nice; the power index metric itself has meaning that makes sense to everyone: the percentage scheme tells us how much better or worse our performance was to average. Anything below 100% is below average for the population, anything over 100% is above average. Rather similar to an IQ measure.
In terms of the top and bottom ranges 140% is going to be elite, where 70% is for the largely untrained.
One last point, you can take the power index and multiply it by 2.61 to get an estimate of Critical Power. Obviously its from one data point only, but should be indicative of where you're at. We use this aspect later when predicting performance in the Banister model.
You can see the overall trend, and this is over 10 years. There are a lot of sub-maximal efforts, this athlete for example, is a long-distance TTer who doesn't perform tests very often and tends to concentrate on volume not intensity.
I'll be honest, this problem is something I have looked at many times in the past. The main intuition that came to me was watching this animation of a convex hull algorithm from wikipedia:
It's filtering out in much the way I'd like, but is a little too efficient, we don't want to weed out all the data otherwise we'll have nothing to model with. We're looking for the maximals, not a hull after all.
If you look on the wiki page you will see its using the same vector cross product trick as Graham's Scan (another convex hull algorithm). This is really useful to see if points are collinear (on the same line) or if we're turning right or left.
I kept this nifty trick, it helps to see what the local trend is. But I added another couple of rules: if the next point has a higher value (power index) then we always keep it, that way we don't trim data we want to keep. Additionally, if it looks like we're turning right, or the next point is lower than this one, look ahead 4 points (a month) and see if there's a better (higher or turning left) point and keep that.
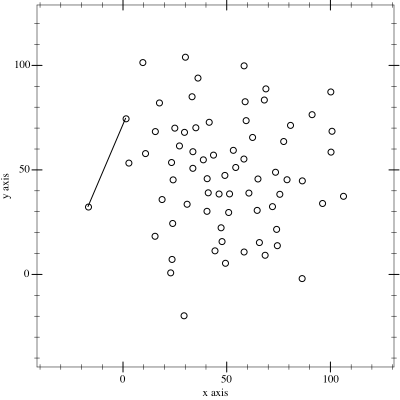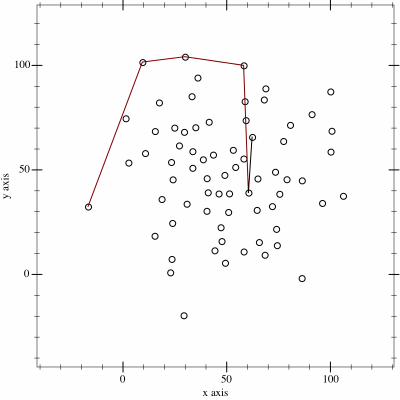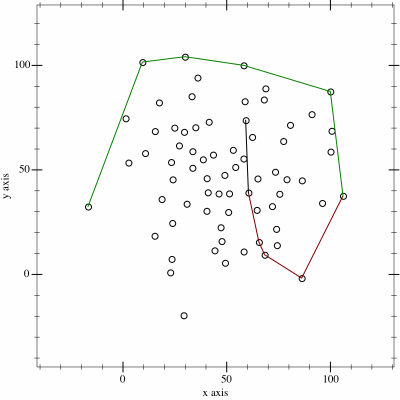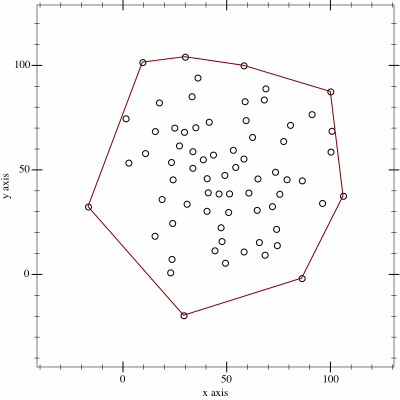
I'm sure the code could be improved - and no doubt will be over time. But it seems to do a good job on the athlete data I've tested it with so far.
Since the data is now no longer equally distributed in the x-axis (date) there is now an unintentional weighting -- this only really affects model fitting, but is an issue. I'll come back to that in the next blogpost on Banister modelling.
Performance testing is useful
When it comes to tracking and modelling performance you can't beat a performance test. Whether it's a set of tests to exhaustion, a 40km TT or just tracking your time up a local hill, they're really useful. If your performance improves then you know your training is working, if your performance goes down then maybe you're fatigued or losing fitness with too little training. Either way you have concrete evidence.And it should be no surprise that performance tests are the main inputs into most performance models. If we want to model and predict maximal performance, generally we need a measure of maximal effort from a performance test.
They hurt, so lets try and avoid them
One of the biggest drawbacks of performance testing is they hurt. You are pushing yourself to the limit during them and this means pain and suffering. Additionally, you'll need you to be rested before you do them and will need some recovery afterwards. As a result, a lot of athletes (and I include elite athletes in the mix) avoid doing maximal exhaustion tests. This causes real problems when we want to track performance since we just don't have reliable data.One way of overcoming this is to design an approach for modelling performance that doesn't need maximal tests. The TrainingPeaks Performance Manager Chart takes this approach. It is based upon the Banister Impulse Response model and provides a measure of likely performance called CTL and measure of likely fatigue called TSB. These measures are related only to the accumulated training load over a long and short duration. Effectively comparing how much training you've been doing over the long haul versus the last few days. Increase load too quickly and you'll fatigue and risk injury, reduce it too much and you'll recover quickly but lose fitness.
By contrast, Banister fits and correlates accumulated training load to performance tests, these are typically 6 minute TTE tests but it can use any measure. It then predicts future performance given a future training load using the coefficients from the fitting process.
These coefficients are effectively what were removed from Banister model to create the PMC. Of course, by doing so this removed the ability to make predictions about future performance. This is fine for tracking overall progression but is rather abstract given the units used don't relate to performance. As a result some coaches try to assign meaning to aspects of the PMC that is akin to tasseography.
Banister is a much more useful tool since it can track progression in concrete terms and predict future performance by learning from our past response. The Banister model isn't perfect and has issues too, one of the biggest is the need for those pesky performance tests.
So, what we really need is a way of using the Banister approach, but without necessarily mandating regular performance testing.
In general, most road cyclists will perform maximal efforts at some point each week. Whether that's a short climb on a favourite loop, a Saturday chain gain with faster riders or just going for a ride over hilly terrain. Some may even perform a regular performance test. If we could find these maximal efforts automatically, we could use them as inputs into models.
I previously blogged about finding sustained efforts in a ride, using a PD model to hunt them down. Well, finding a maximal effort takes a similar approach. Only this time I'm not going to need to know anything about the athlete. I need to extract these maximal efforts purely from the raw data.
That's what this blogpost is going to describe, eventually.
Rouleurs and Puncheurs and Sprinteurs, oh my!
I need to digress to the topic of the power duration relationship and how it differs across all cyclists. For a more in depth treatment I urge you to read Mike Puchowiz blogpost, which I am going to summarise here.We all know that some cyclists have a better sprint than others, some are better at time-trialling and some seem to be more punchy or better at climbing. So much so that cycling has a lexicon to describe them; 'sprinteurs', 'rouleurs', 'puncheurs' and 'grimpeurs'. Putting weight and height to one side, ultimately the athlete type is characterised by the shape of their power duration curve. Sprinters typically have a high Pmax and W', TTers have a high CP regardless of weight, puncheurs maintain high power for much longer.
So, around Christmas 2018, Mike downloaded the MMP data for all the athletes in the GC opendata set (around 2,500 seasons of a 100 or more workouts) and performed a Functional Principal Component Analysis on them.
The analysis identified 3 parts of the PD relationship that explain over 90% of the variation in all cyclists. The aspects that differentiate the rouleurs, puncheurs and so on. They are:
- PC1 - Capability - it simply raises or lowers the overall curve. This is equivalent to Critical Power of course. It represents 75% of all variance across the population.
- PC2 - Twitchiness - is the athlete endurance dominant or sprint dominant. This is kind of equivalent to W'. It represents 15% of all variance across the population.
- PC3 - Sprint Endurance - is the duration maximal power can be maintained. This has no real equivalent in the CP model. It represents about 2.5% of all variance across the population.
The average athlete
Also, during the last few months of 2018 I did some data profiling using the GoldenCheetah opendata. One aspect of this was to profile the entire PD relationship and identify the upper and lower bounds across all athletes. This was then published as a spreadsheet.I also found the average (male) athlete; a Critical Power of 261w, a W' of 15.5kj and a Pmax of 1100w.
Power Index
Given a selection of intervals, how do you decide which indicates better performance (read higher Critical Power). If I have a 4minute effort for 300w a 10minute effort for 250w and a 20min effort for 240w, which is the peak?The Power Index of any power duration point will tell us, it is effectively the same thing as the PC1 from the FPCA above.
It is the power for the interval duration expressed as a percentage of the predicted power for the same interval duration we get for the average athlete.
The prediction can come from any PD model, it doesn't matter too much so long as the PD model is relatively reliable. For the implementation in GC I used the Morton 3 parameter model. I could avoid a model altogether and use the 50th quartile MMP data from the Opendata analysis. But using a model is quick and easy enough to implement.
So as a worked example, lets look at the 3 intervals above, and see how they come out. First, to predict power for an interval with duration t:
P(t) = W' / t - W'/CP-Pmax + CP
So plugging the numbers into the formula, the predicted power for 4, 10 and 20 minute intervals, for our average athlete (CP=261w, W'=15.5kj, Pmax=1100w) are shown below, along with the average powers from above, the calculated power index percentage and rank:
The 4min effort is the best, but those 10 and 20minute efforts are a close run thing. In practice, to isolate the impact of the other principal components it only makes sense to work with intervals between 3 and 20 minutes. Which rather helpfully maps quite nicely onto the CP models. So, in summary we have a metric that can be used to rank intervals between 3 and 20 minutes to extract the very best efforts.One other aspect of this is quite nice; the power index metric itself has meaning that makes sense to everyone: the percentage scheme tells us how much better or worse our performance was to average. Anything below 100% is below average for the population, anything over 100% is above average. Rather similar to an IQ measure.
In terms of the top and bottom ranges 140% is going to be elite, where 70% is for the largely untrained.
One last point, you can take the power index and multiply it by 2.61 to get an estimate of Critical Power. Obviously its from one data point only, but should be indicative of where you're at. We use this aspect later when predicting performance in the Banister model.
Submaximal Filtering Algorithm
So once I extract the weekly best interval across all athlete data I find there are some weeks where the athlete didn't actually work maximally. When eyeballing the data I can see a general trend, but how to isolate out the submaximal efforts?
I'll be honest, this problem is something I have looked at many times in the past. The main intuition that came to me was watching this animation of a convex hull algorithm from wikipedia:
Image: Maonus [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)] from Wikimedia Commons
It's filtering out in much the way I'd like, but is a little too efficient, we don't want to weed out all the data otherwise we'll have nothing to model with. We're looking for the maximals, not a hull after all.
If you look on the wiki page you will see its using the same vector cross product trick as Graham's Scan (another convex hull algorithm). This is really useful to see if points are collinear (on the same line) or if we're turning right or left.
I kept this nifty trick, it helps to see what the local trend is. But I added another couple of rules: if the next point has a higher value (power index) then we always keep it, that way we don't trim data we want to keep. Additionally, if it looks like we're turning right, or the next point is lower than this one, look ahead 4 points (a month) and see if there's a better (higher or turning left) point and keep that.
I'm sure the code could be improved - and no doubt will be over time. But it seems to do a good job on the athlete data I've tested it with so far.
Since the data is now no longer equally distributed in the x-axis (date) there is now an unintentional weighting -- this only really affects model fitting, but is an issue. I'll come back to that in the next blogpost on Banister modelling.